Laufzeit

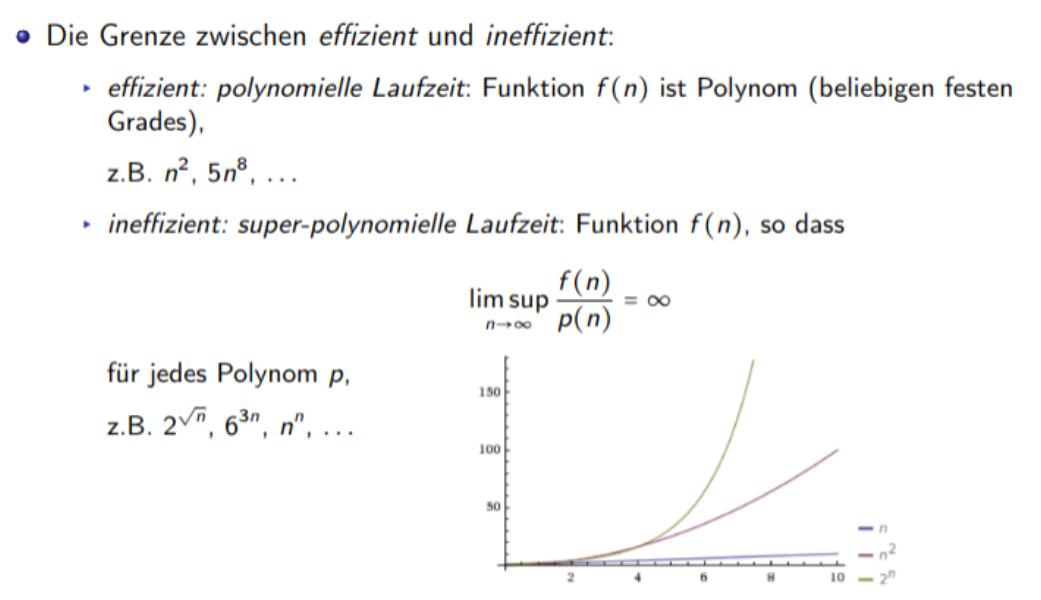
Polynomielle vs super-polynomielle Laufzeit

Link to original

O-Notation

Sei $g:\mathbb{N}\to \mathbb{R}$ eine Funktion.

\{ f: \mathbb{N} \rightarrow \mathbb{R} \; | \; \exists c \in \mathbb{R}_{+} : \exists n_{0} \in \mathbb{N} : \forall n \geq n_{0} : f(n) \leq c \cdot g(n) \}$$ ![[Pasted image 20231109154107-0.png]] > Groß-O liefert obere Schranke an die Komplexit¨at einer Funktion. ## Rechnen mit [[O-Notation]] ![[Pasted image 20231109154453-0.png]] ![[Pasted image 20231109154602-0.png]]Link to original

Ω-Notation

Sei $g:\mathbb{N}\to \mathbb{R}$ eine Funktion.

\{ f: \mathbb{N} \rightarrow \mathbb{R} \; | \; \exists c \in \mathbb{R}_{+} : \exists n_{0} \in \mathbb{N} : \forall n \geq n_{0} : f(n) \geq c \cdot g(n) \}$$ ![[Pasted image 20231109154907-0.png]]Link to original

Laufzeit-Notationen

Funktionen die asymptotisch nicht schneller als g wachsen

\{f: \mathbb{N} \rightarrow \mathbb{R} \; | \; \textcolor{yellow}{\exists} c \in \mathbb{R}_{+} : \exists n_{0} \in \mathbb{N} : \forall n \geq n_{0} : f(n) \textcolor{yellow}{\leq} c \cdot g(n)\}$$ > Funktionen die asymptotisch **nicht langsamer** als g wachsen $$\mathcal{\Omega}(g) := \{f: \mathbb{N} \rightarrow \mathbb{R} \; | \; \textcolor{yellow}{\exists} c \in \mathbb{R}_{+} : \exists n_{0} \in \mathbb{N} : \forall n \geq n_{0} : f(n) \textcolor{yellow}{\geq} c \cdot g(n)\}$$ > Funktionen die asymptotisch das **gleiche** Wachstum wie g haben $$\mathcal{\Theta}(g) := \mathcal{O}(g) \cap \mathcal{\Omega}(g)$$ > Funktionen die asymptotisch **langsamer** als g wachsen $$\mathcal{o}(g) := \mathcal{O}(g) \backslash \mathcal{\Omega}(g)$$ $$\Rightarrow \{f: \mathbb{N} \rightarrow \mathbb{R} \; | \; \textcolor{yellow}{\forall} c \in \mathbb{R}_{+} : \exists n_{0} \in \mathbb{N} : \forall n \geq n_{0} : f(n) \textcolor{yellow}{\leq} c \cdot g(n)\}$$ > Funktionen die asymptotisch **schneller** als g wachsen $$\mathcal{\omega}(g) := \mathcal{O}(g) \backslash \mathcal{\Omega}(g)$$ $$\Rightarrow \{f: \mathbb{N} \rightarrow \mathbb{R} \; | \; \textcolor{yellow}{\forall} c \in \mathbb{R}_{+} : \exists n_{0} \in \mathbb{N} : \forall n \geq n_{0} : f(n) \textcolor{yellow}{\geq} c \cdot g(n)\}$$ [[Laufzeit]]Link to original