Mat3 Blatt 10

Gruppe: 7
Maarten Behn, Niklas Borchers, Emre Kilinc

Aufgabe 37: Skalentypen

Angenommen, in einer Gruppe von Informatik-Studierenden werden (im Rahmen der Bevölkerungsforschung) verschiedene Merkmale erhoben. Geben Sie für die nachstehenden Merkmale jeweils den zugehörigen Skalentyp des Merkmals an und begründen Sie Ihre Antworten

(a) Anzahl Fachsemester

→ Verhältnisskala
Die Anzahl der Fachsemester ist eine zählbare Größe mit natürlichem Nullpunkt und sinnvollen Verhältnisaussagen.

(b) Bundesland des Erstwohnsitzes (bzw. Land bei Ausland)

→ Nominalskala
Die Merkmalsausprägungen sind Namen oder Kategorien, zwischen denen keine Rangfolge oder arithmetische Operation möglich ist.

(c) Durchschnittsnote bei den bestandenen Modulprüfungen

→ Ordinalskala
Aus der Vorlesung:
“Ein klassisches Beispiel für ein ordinalskaliertes Merkmal sind Schulnoten. Zwar weiß man, dass die Note 1 besser ist als die Note 2, aber der Abstand zwischen 1 und 2 lässt sich sicherlich nicht interpretieren oder vergleichen etwa mit demjenigen zwischen 4 und 5.”

(d) Verfügbares Monats-Nettoeinkommen (in Euro und Cent)

→ Verhältnisskala
Das Einkommen ist eine metrische Größe mit natürlichem Nullpunkt und interpretierbaren Verhältnissen.

Aufgabe 38: Beschreibende Statistik

Bei der Messung der Körpergröße von 20 männlichen Schülern ergaben sich die folgenden Werte (in cm):

149 147 158 165 153 153 168 158 163 159   
177 175 163 170 162 162 170 153 147 157  

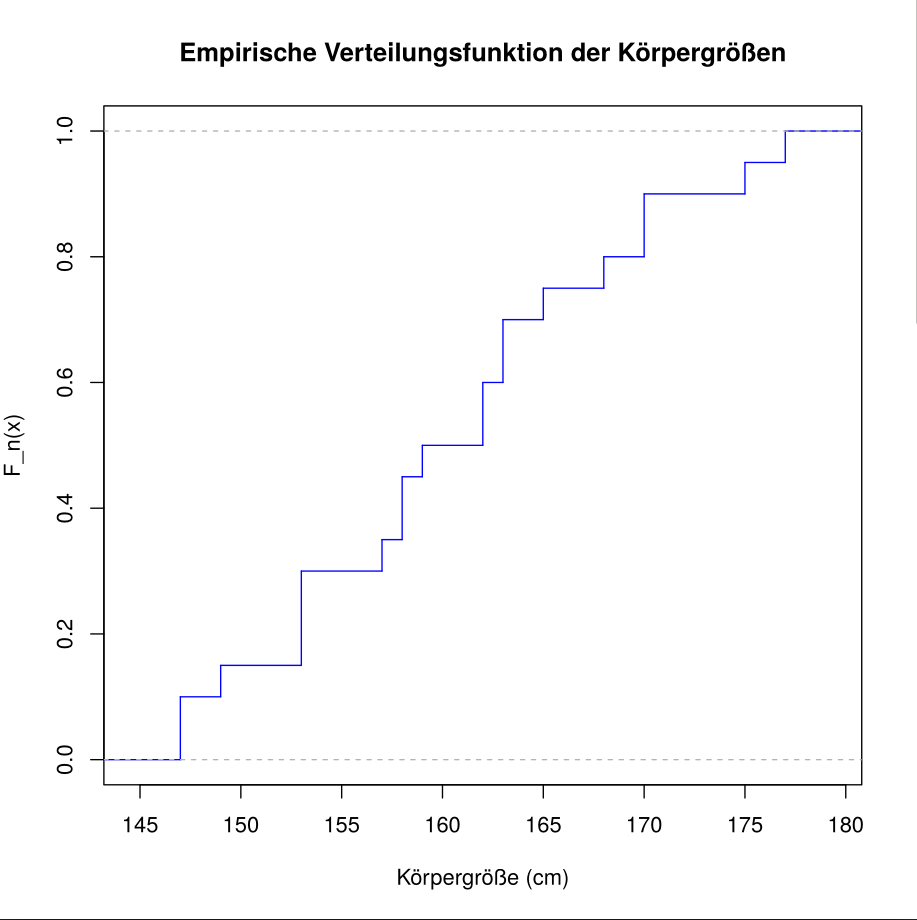
(a) Zeichnen Sie die empirische Verteilungsfunktion der angegebenen Messreihe (von Hand).

Sortierte Werte:
147, 147, 149, 153, 153, 153, 157, 158, 158, 159,
162, 162, 163, 163, 165, 168, 170, 170, 175, 177

Sei $x_1,\dots ,x_n$ die Messreihe ($n=20$), dann gilt:

Die empirische Verteilungsfunktion ist stückweise konstant und steigt bei jedem Wert um $\frac{1}{20}$ an.

$${\hat{F}}_n(x)=\frac{1}{20}\cdot \#\{i:x_i\le x\}$$

R code zum vergleichen:

x <- c(149, 147, 158, 165, 153, 153, 168, 158, 163, 159,   
       177, 175, 163, 170, 162, 162, 170, 153, 147, 157)  
  
x_sorted <- sort(x)  
  
edf <- ecdf(x)  
  
plot(edf, main = "Empirische Verteilungsfunktion der Körpergrößen",  
     xlab = "Körpergröße (cm)", ylab = "F_n(x)", col = "blue",  
     verticals = TRUE, do.points = FALSE)  

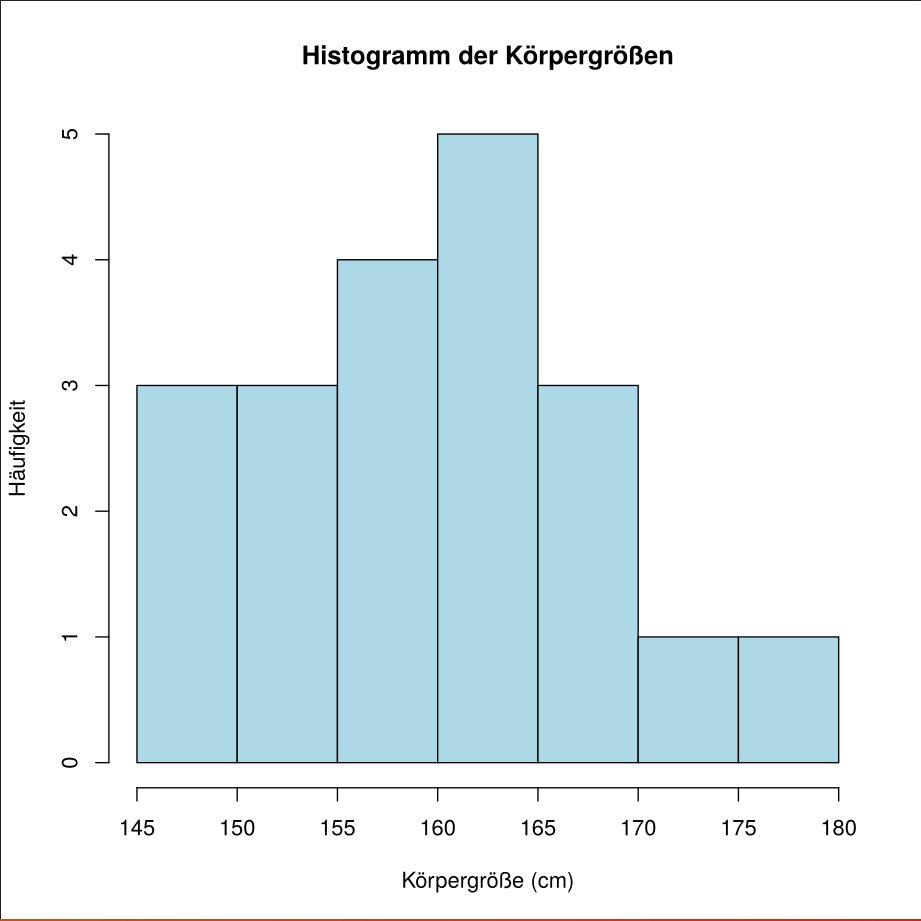
(b) Zeichnen Sie ein Histogramm der angegebenen Messreihe mit der folgenden Klasseneinteilung: $(145,150],(150,155],...,(175,180]$.
(c) Zeichnen Sie ein gleitendes Histogramm der angegebenen Messreihe.

Klassen:

• $(145,150]$: 3 Werte $(147,147,149)$

• $(150,155]$: 3 Werte $(153,153,153)$

• $(155,160]$: 4 Werte $(157,158,158,159)$

• $(160,165]$: 5 Werte $(162,162,163,163,165)$

• $(165,170]$: 3 Werte $(168,170,170)$

• $(170,175]$: 2 Werte $(175,177)$

R code zum vergleichen:

x <- c(149, 147, 158, 165, 153, 153, 168, 158, 163, 159,   
       177, 175, 163, 170, 162, 162, 170, 153, 147, 157)  
  
breaks <- seq(145, 180, by = 5)  
  
hist(x, breaks = breaks, right = TRUE,  
     main = "Histogramm der Körpergrößen",  
     xlab = "Körpergröße (cm)", ylab = "Häufigkeit",  
     col = "lightblue", border = "black")  
       
dens <- density(x, bw = "nrd0")  
  
plot(dens, main = "Gleitendes Histogramm (Kerndichteschätzung)",  
     xlab = "Körpergröße (cm)", ylab = "Dichte", col = "darkgreen", lwd = 2)  
polygon(dens, col = "lightgreen", border = "darkgreen")  

(d) Berechnen Sie die empirische Schiefe des Merkmals ”Körpergröße von männlichen Schülern“ anhand der angegebenen Messreihe und interpretieren Sie Ihr Ergebnis anhand der erstellten Graphiken.

Mittelwert:

$$\bar{x}=\frac{1}{20}\sum _{i=1}^{20}{x}_i=\frac{3209}{20}=160.45\text{cm}$$

Empirische Standardabweichung:

$$s=\sqrt{\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x}{)}^2}\approx 8.73\text{cm}$$

Empirische Schiefe:

$$g_1=\frac{1}{n}\sum _{i=1}^n{\left(\frac{x_i-\bar{x}}{s}\right)}^3\approx 0.197$$

$g_1>0$ →leicht positive Schiefe

Was in den Zeichnungen erkennbar ist:

• Die empirische Verteilungsfunktion steigt im oberen Bereich etwas langsamer an.
• Das Histogramm zeigt mehr Werte im unteren und mittleren Bereich, während der obere Bereich (ab 170 cm) dünner, aber vorhanden ist.
• Das gleitende Histogramm hat seinen maximal wert weiter links.

Aufgabe 39: Programmieraufgabe (R)

Der in dem Foliensatz zur deskriptiven Statistik besprochene Datensatz zum ”Old Faithful“- Geysir ist in R mit dem Namen faithful enthalten. Veranschaulichen Sie sich die univariaten Verteilungen der beiden Variablen ”Eruptionsdauer“ und ”Wartezeit bis zum Ausbruch“ anhand geeigneter Kennzahlen und Graphiken.

data("faithful")  
  
cat("eruptions:\n")  
cat("Min: ", min(faithful$eruptions), "\n")  
cat("Max: ", max(faithful$eruptions), "\n")  
cat("Standard Abweichung: ", sd(faithful$eruptions), "\n")  
cat("Mean: ", mean(faithful$eruptions), "\n")  
cat("Median: ", median(faithful$eruptions), "\n")  
cat("Mad: ", mad(faithful$eruptions), "\n")  
  
cat("\nwaiting:\n")  
cat("Min: ", min(faithful$waiting), "\n")  
cat("Max: ", max(faithful$waiting), "\n")  
cat("Standard Abweichung: ", sd(faithful$waiting), "\n")  
cat("Mean: ", mean(faithful$waiting), "\n")  
cat("Median: ", median(faithful$waiting), "\n")  
cat("Mad: ", mad(faithful$waiting), "\n")  
  
hist(faithful$eruptions, breaks = 20, col = "lightblue",  
     main = "Histogramm der Eruptionsdauer",  
     xlab = "Dauer (Minuten)", ylab = "Häufigkeit")  
  
hist(faithful$waiting, breaks = 20, col = "lightgreen",  
     main = "Histogramm der Wartezeit",  
     xlab = "Wartezeit (Minuten)", ylab = "Häufigkeit")  
  
plot(density(faithful$eruptions), main = "Dichte: Eruptionsdauer", xlab = "Dauer (Minuten)", col = "blue")  
plot(density(faithful$waiting), main = "Dichte: Wartezeit", xlab = "Wartezeit (Minuten)", col = "darkgreen")  
  

Output:

eruptions:  
Min:  1.6  
Max:  5.1  
Standard Abweichung:  1.141371  
Mean:  3.487783  
Median:  4  
Mad:  0.9510879  
  
waiting:  
Min:  43  
Max:  96  
Standard Abweichung:  13.59497  
Mean:  70.89706  
Median:  76  
Mad:  11.8608  

40. Multiple Select-Aufgabe.

Betrachten Sie die folgenden Aussagen über empirische Verteilungen und empirische Verteilungsfunktionen.
Dazu seien $Y_1,...,Y_n$ reellwertige, identisch verteilte Zufallsvariablen mit Verteilungsfunktion $F$ von $Y_1$ und mit empirischer Verteilungsfunktion ${\hat{F}}_n$ von $Y_1,...,Y_n$.

a) Falls $Y_1,...,Y_n$ nicht stochastisch unabhängig sind, so kann es (mit nicht vernachlässigbarer Wahrscheinlichkeit) passieren, dass ${\hat{F}}_n$ die wahre Verteilungsfunktion $F$ selbst für großes $n$ nicht präzise approximiert.

Ja,
denn die empirische Verteilungsfunktion ${\hat{F}}_n$ ist nur dann ein konsistenter Schätzer für $F$, wenn gewisse Voraussetzungen wie (mindestens asymptotische) Unabhängigkeit und identische Verteilung erfüllt sind.

b) Falls $Y_1,...,Y_n$ nominalskaliert sind, so lassen sich $F$ und ${\hat{F}}_n$ nicht sinnvoll interpretieren.

Nein,
auch bei Nominalskalen ist ${\hat{F}}_n$​ interpretierbar – nur die Ordnung ist nicht natürlich.

c) Falls $Y_1,...,Y_n$ dichotom sind, so lässt sich ${\hat{F}}_n$ nicht sinnvoll interpretieren.

Nein,
Dichotome Zufallsvariablen nehmen nur zwei Werte an.
Auch in diesem Fall ist die empirische Verteilungsfunktion ${\hat{F}}_n$ sinnvoll interpretierbar:
Sie gibt an, wie viele Beobachtungen kleiner oder gleich einem bestimmten Wert sind.

• Beispielsweise:

$${\hat{F}}_n(y)=\{\begin{array}{ll}0& \text{fu¨r }y<0\\ p_n& \text{fu¨r }0\le y<1\\ 1& \text{fu¨r }y\ge 1\end{array}$$

wobei $p_n$ der Anteil der Nullen ist.

d) Falls $Y_1,...,Y_n$ intervallskaliert sind, so lässt sich aus ${\hat{F}}_n$ ein Histogramm der empirischen Verteilung von $Y1,...,Yn$ ableiten.

Ja,
Intervallskalierte Daten besitzen eine sinnvolle Ordnung und Abstände, daher kann man aus der empirischen Verteilungsfunktion ${\hat{F}}_n$ die relative Häufigkeit in beliebigen Intervallen bestimmen:
Für ein Intervall $[a,b]$ gilt:

$$\text{relative Ha¨ufigkeit in }[a,b]={\hat{F}}_n(b)-{\hat{F}}_n(a)$$

Damit lassen sich Balken eines Histogramms konstruieren, wenn die Daten in Klassen (z.B. Intervalle) eingeteilt werden.