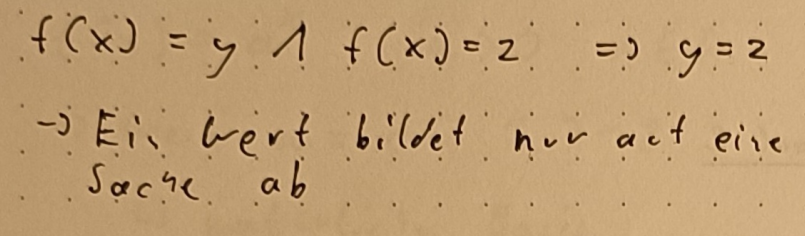up:: Mat1 MOC

Quelle:
20221028_TH_M1-Skript_v02-3.pdf

Relation

Relation (R) ist die Teilmenge eines katesischen Produkt.

Seinen A und B Mengen. Dann heißt jede Teilmenge $R\subseteq A\times B$ Relation zwischen A und B. Ist $A=B$, also $R\subseteq A\times A$ dann heißt R Relation auf A. Gilt $(a,b)\in R$, so sagt man “a steht in Relation zu b”.

$aRb$ statt $(a,b)\in R$ denn ist lesbarer
Beispiel: $=$
$a=b$ statt $(a,b)\in =$ und $=\subseteq M\times M$

Eigenschaften von Relationen

reflexiv

wenn für alle $x\in A$ gilt: $xRx(x=x)$

Link to original

symmetrisch

wenn für alle $x,y\in A$ gilt: $xRy⟹yRx(x=y⟹y=x)$

Link to original

antisymmtrisch

wenn für alle $x,y\in A$ gilt: $xRy\wedge yRx⟹x=y$
Antisymmtrisch ist nicht das Gegenteil von symemtrisch. ($=$ ist beides)

Link to original

transitiv

wenn für alle $x,y,z\in A$ gilt: $xRy\wedge yRx⟹xRz$

Link to original

total

wenn für alle $x,y\in A$ gilt: $xRy\vee yRx$

Link to original

Arten von Relationen

Art	reflexiv	symmetrisch	antisymmtrisch	transitiv	total	Beispiel
Äquivalenzrelation	x	x		x		=
Halbordnung	x		x	x		$\subseteq$
totale Ordnung	x		x	x	x	$\le$

Relationen zwischen zwei Mengen

funktional

Eine Relation $R\subseteq M\times N$ zwischen zwei Mengen $M$ un $N$ heißt
funktional (oder rechtseindeutig) wenn für alle $x\in M$ und $y,z\in N$ gilt: $xRy\wedge xRz⟹y=z$

Link to original

⇒ Ein Wert bildet nicht auf zwei Sachen ab.

linkstotal

Eine Relation $R\subseteq M\times N$ zwischen zwei Mengen $M$ un $N$ heißt
linkstotal, wenn gilt:$M=\{x\in M|\exists y\in N:xRy\}$

Link to original

⇒ Jeder Wert bildet einmal ab.